Covid 19 and Exponentials
Many of my students often ask me: why are exponentials and logarithms important? Well, there is no better time to really appreciate the importance of these functions than right now during The Great Pandemic of 2020. The spread of viruses follows exponential behavior, as do many other physical, social, and economic processes. So let’s learn a bit about exponentials. You’re all familiar with ex. This is, of course, a very special function (namely because the slope = the value). But there are lots of other ways to write an exponential.
For instance, imagine you invest $1000 in a stock that increases by 25% per year. How much money do you have after 10 years? You might think you’ll have 10 × 25% = 250%. Take this and multiply by $1000 and you’ll have $2500. But THIS IS WRONG. Why? Because after the first year, you should multiply $1000 × 1.25 = $1250. And the next year you multiply this again, $1250 × 1.25 = $1562. And so on. The formula you need is this: $Final = $1000 × (1+.25)years. If you plug in years = 10, you get a whopping $9313 !!! (So start investing now). This is the power of exponential growth.
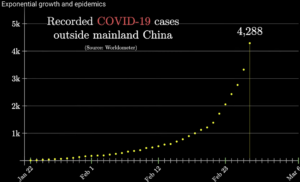
So what happens with viruses? Well, they scale the same way. That is, the numbers scale like (1 + infection rate)time. There’s not much we can do about time, so the only way to beat this is to lower the infection rate, which is why you are probably all isolated at home right now.
There is, of course, more to this story. And for a great explanation, I highly suggest the following video: Exponential Growth and Epidemics.
We wish you all peace and good health.
Dr. A and Learning Glass Team